KI für Zeitreihen: Modelltypen (Teil 1)
aus der Reihe: “Die Evolution der Künstlichen Intelligenz für sequenzielle Daten”
In unserem ersten Blog-Beitrag der Reihe haben wir einen Blick auf die Natur sequenzieller Daten und die besonderen Charakteristika von Zeitreihen geworfen. Beginnend mit diesem Artikel widmen wir uns nun verschiedenen Ansätzen, mit denen sich solche Daten modellieren lassen.
Was bedeutet ‘Modellieren’? Was zeichnet ein KI-Modell aus?
Das Ziel der Anwendung von Künstlicher Intelligenz im analytischen Bereich ist immer die bestmögliche Erfassung der in den Daten liegenden Information, d.h. der Zusammenhänge zwischen den einzelnen Datenpunkten. Ein optimales Modell würde alle Zusammenhänge in den Trainingsdaten erkennen, also in den Daten, aus denen das Modell “lernt” (oder treffender: mit denen es “angelernt wird”). Vorausgesetzt, dass die Trainingsdaten alle möglichen Fälle abdecken, kann das trainierte Modell diese Zusammenhänge auch in neuen Daten wiederfinden, solange sie unter den gleichen Rahmenbedingungen aufgenommen werden. Auf dieser Basis kann es beispielsweise entscheiden, ob die Qualität eines Werkstücks abdriftet, oder ob sich die Lebensdauer eines Maschinenteils ihrem Ende nähert. Da die Zusammenhänge in Daten völlig unterschiedlicher Natur sein können, gibt es keine allgemeingültige Regel, nach der sich ein optimales Modell konstruieren lässt. Im Laufe der Zeit sind daher sehr viele unterschiedliche Typen oder Klassen von Modellen entstanden. Wir beschränken uns in dieser Serie auf Modellklassen, die sich für Zeitreihen und andere sequenzielle Daten eignen.
Autoregressive Sequenzmodelle
Eine etablierte Methode zur Vorhersage von Zeitreihendaten sind die statistisch motivierten ARIMA- und SARIMA-Modelle. Sie beruhen im Wesentlichen auf einer Korrelationsanalyse der Daten, d. h. sie bestimmen den statistischen Zusammenhang zwischen aktuellen und vorherigen Datenpunkten der jeweiligen Zeitreihe. Nach dem Training erhält man ein Modell, das aus den Koeffizienten bzw. Gewichten für die unterschiedlich weit zurückliegenden Werte besteht (dies ist der autoregressive “AR”-Teil), sowie aus weiteren Gewichten, die auftretende Abweichungen ausgleichen sollen (der moving average “MA”-Teil).
Da Zeitreihen häufig langfristige Trends und saisonale Schwankungen aufweisen, wurde das ursprüngliche ARMA-Modell so modifiziert, dass diese Einflüsse zu einem Teil berücksichtigt werden können (integrated “I”, seasonal “S”). Dazu sind jedoch manuelle Eingriffe in die Daten und in die Modellparameter erforderlich.
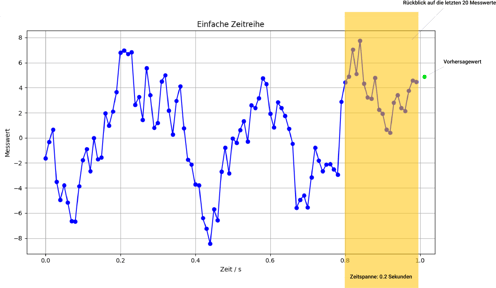
Im Beispiel der abgebildeten Zeitreihe würde ein (S)ARIMA-Modell zu jedem Zeitpunkt auf die letzten n = 20 Messwerte zurückblicken, um daraus eine Vorhersage des nächsten Wertes zu berechnen. Welche der 20 Werte tatsächlich herangezogen werden, hängt von der durch das Training ermittelten Gewichtung der jeweiligen Zeitabstände ab. Es lässt sich intuitiv erahnen, dass die feste Gewichtung bestimmter Zeitabstände nicht immer zu einer optimalen Vorhersage führen wird. Der Vorteil dieses Modelltyps besteht in der Nachvollziehbarkeit der Vorhersagen und dem vergleichsweise einfachen Training.
Zusammengefasst:
- (S)ARIMA-Modelle bilden die statistische Korrelation zwischen unterschiedlich weit zurückliegenden und aktuellen Datenpunkten ab.
- Sie sind gut für Menschen interpretierbar.
- Feste Modellparameter führen mit der Zeit zu suboptimalen Vorhersagen, dynamische Parametrierungen erfordern manuellen Aufwand.
- Die Flexibilität von (S)ARIMA-Modellen ist insgesamt nicht so groß wie bei Deep-Learning-Methoden, denen wir uns in den kommenden Artikeln zuwenden werden.

